Təkdəyişənli Xətti Reqresiya Modelinə Bir Nümunə

İnsanlar həyatdakı ehtiyaclarını qarşılamaq üçün müəyyən yaşdan sonra hər hansı bir işdə işləməyə başlayır. Təbii ki, gördüyü işi müəyyən maaş qarşılığında edir. O insanın maaşı isə, onun işindəki iş məhsuldarlığından asılıdır. İş məsuldarlığı, bir çox faktorla yanaşı həm də insanın yaşından asılıdır. Bir insanın yaşı onun iş məhsuldarlığına, dolayısı ilə onun aldığı maaşa necə təsir edir? Nəzəriyəyə görə, yaşla iş məhsuldarlığı arasında artan şəkildə bir əlaqə vardır. Yəni bir insanın yaşı artdıqca onun iş məhsuldarlığı da artmış olur. Bu artıma səbəb, illər keçdikcə insanın işində qazandığı təcrübədir.

Bu söylənilənlərin parktik cəhətdən doğruluğunu yoxlamaq üçün təkdəyişənli ekonometrik model istifadə edilir. Modeldə istifadə ediləcək datalar, tam işgünü çalışmaq şərti ilə daimi işlə təmin olunmuş 25-34 yaşları arasındakı insanlar arasında keçirilmiş anket soğrusunun nəticələrinə əsaslanır. 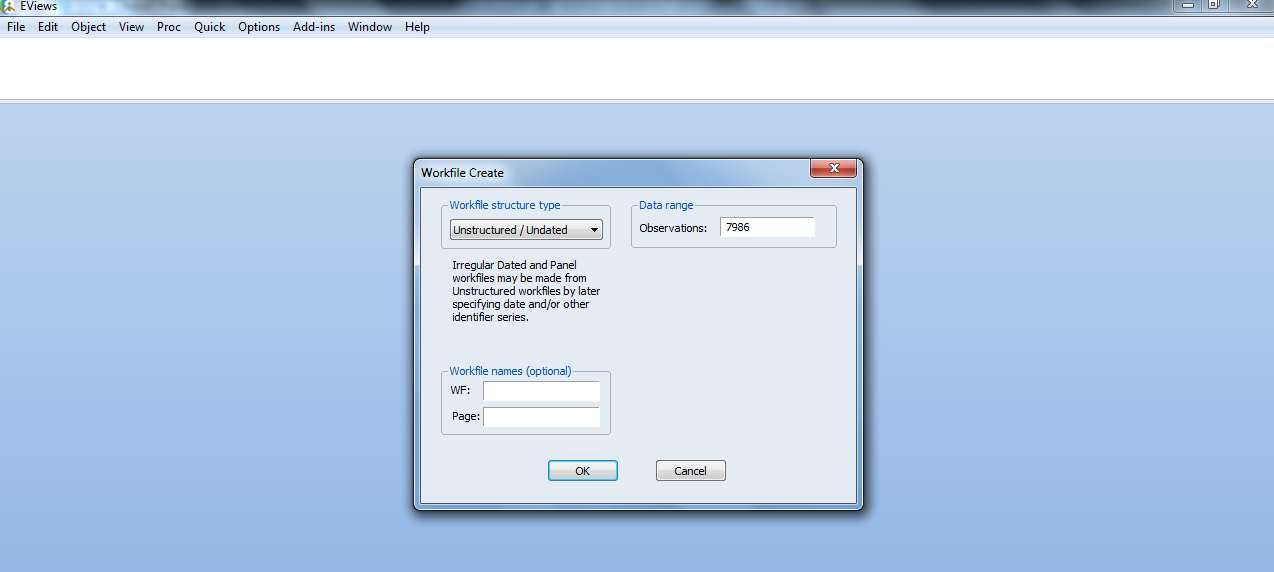Bu datalar hər il ABŞ-da “Labor of Bureau Statistics” tərəfindən təxminən  65.000 ailə arasında aparılmış anket sorğusundan təsadüfi seçmə metodu ilə seçilmiş 7986 müşahidə dəyərindən ibarətdir. Sözü gedən ekonmetrik modelin ümumi şəkli və istifadə edilən dəyişənlərə aid paylanma qrafiki aşağıdakı kimidir.

Burada OSQ dəyişəni asılı dəyişən olub ortalama saatlıq qazancı, YASH dəyişəni isə sərbəst dəyişən olmaqla anket soğrusunda iştirak edən insanların yaşlarını göstərməkdədir. β₁ və β₂ müvafiq olaraq kəsişmə və meyl əmsalını, u_i isə xəta terminini ifadə edir. i indeksi isə, insanların anketdəki nömrəsini göstərir. Qrafikdən göründüyü kimi, anket sorğusunda iştirak edənlər arasında eyni yaşda olan insanların ortalama saatlıq qazancları fərqlidir. Ən yüksək ortalama saatlıq qazanca sahib şəxsin yaşı 31, ortalama saatlıq qazancı isə 61 dollardır. Bu deyilənləri hər iki dəyişənə aid olan təsviri statistik göstəricilərdən də görmək olar.

Modeli Eviews programında təxmin etmək üçün ilk öncə dataların proqrama girilməsi zəruridir. Eviews programı açıldıqda ilk öncə, iş faylı açılır(workfile). Daha sonra üzərində çalışacağımız datanın tipi və müşahidə sayı girilir. Bu addımlardan sonra isə datalar ya əllə, ya da hər hansı bir excel faylından Eviews programına çağrılır. Yuxarıda göstərilən mərhələlər aşağıdakı pəncərələrdə praktik olaraq göstərilmişdir.

Bu addımlardan sonra sıra modelin təxmin edilməsindədir. Modelin necə təxmin ediləcəyi menyular vasitəsi ilə aşağıda göstərilmişdir.

Ən kiçik kvadratlar metoduna görə təxmin edilmiş modelimiz aşağıdakı şəkildə yazıla bilər.

OSQ = 3.32418408995 + 0.451931318807*YASH

Modelin nəticələrinə görə, YASH(yaş) bir vahid artdığı zaman OSQ(ortalama saatlıq qazanc) 0.452 vahid (45.2 sent) artır.

Ekonometrik modellərdə modelin inamlı bir model olması üçün, təxmin edilən modelin iki testdən keçməsi lazmıdır. Bunlardan biri praktik olaraq əldə edilmiş nəticələrin nəzəri məlumatlarla eynilik təşkil etməsi, digəri isə, təxmin edilmiş əmsalların statistik baxımdan inamlı olmasıdır.

Təxmin edilmiş modelin nəticələrinə görə, yaş  ilə maaş(ortalama saatlıq qazanc) arasında müsbət yönlü bir əlaqə vardır. Əldə edilən bu praktik nəticə nəzəri olaraq verilən bilgi ilə üst-üstə düşür. 

Modeldən əldə edilən əmsalların statistik testləri isə, müvafiq əmsallara aid t statistikası və porb dəyərinə (ehtimal dəyəri) əsaslanır. 

Hipotez testi

Statistik hipotez testinin başlanğıc nöqtəsi sıfır hipotezi adlandırılır. Bu hipotez test ediləcək hipotezin müəyyənləşdirilməsinə əsaslanır. Hipotez testi, sıfır hipotezini alternatif hipotez olaraq adlandırılan ikinci bir hipotezlə qarşılaşdırmaq üçün datalardan istifadə etmək zərurətini ortaya çıxarır. Sıfır hipotezi etibarlı olmadığı halda alternatif hipotez qəbul edilir.

t statistikası

t statistikası istənilən modeldə yer alan hər hansı bir dəyişənin müəyyən dəyərə qarşı test edilməsinə imkan verir. t statistikasının düsturu aşağıdakı şəkildə ifadə edilir.

Bu düsturla əldə edilən t statistika dəyəri hesablanış dəyər adlandırılır. Bu dəyər t statistikasına ait cədvəldən əldə edilən kritik dəyərlə qarşılaşdırılır. Əgər t statistikasının hesablanmış dəyəri, cədvəldən əldə edilən dəyərdən böyük olarsa sıfır hipotezi rədd edilir.

Modelimizlə əlaqəli hipotezlər

H₀:=Yaş artımının maaş(ortalama saatlıq qazanc) üstündə bir təsiri yoxdur

H₁:=Yaş artımının maaş(ortalama saatlıq qazanc) üstündə bir təsiri vardır

Bu hipotezlər riyazi olaraq hipotezlərə müvafiq β₂=0 və β₂≠0 şəklində göstərilə bilər. β₂=0 olması Yaş dəyişəninin maaş üzərində bir təsirə sahip olmadığını göstərir. Yuxarıda söylənənlərdən istifadə edərək hipotezlərimizdən hansının etibarlı olduğunu test edək. 

 t cədvəl dəyəri isə R. A. Fisher tərəfindən hazırlanan aşağıdakı cədvəldən tapılır. Bu dəyər sərbəstlik dərəcəsi(səbəstlik dərəcəsi= müşahidə sayı-təxmin edilən parametr sayı) və əhəmiyyətlilik səviyyəsinə (significance level) görə müəyyən edilir. t statistika cədvəli aşağıda verilmişdir.

Bu cədvəldən istifadə qaydası isə belədir.İlk sütunda göstərilən sərbəstlik dərəcəsi sayı ilə əvvəlcədən müəyyən edilmiş əhəmiyyətlilik dərəcəsinin kəsişdiyi nöqtədəki dəyər bizim t kritik dəyərimiz olacaqdır. Bizim modeldə müşahidə sayı 7986, təxmin edilən əmsal sayı 2 olduğundan sərbəstlik dərəcəsi 7984' ə bərabərdir. 95%-lik əhəmiyyətlilik dərəcəsi və 7984 sərbəstlik dərəcəsində t statistikasının kritik dəyəri 1.645'ə bərabərdir. İndi isə hesablanmış t statistikası və t kritik dəyərlərini qarşılaşdırmaqla hipotez testlərindən hansının etibarlı hansının etibarsız olduğuna qərar verəcəyik.

t(hes)=13.48>t(kritik)=1.645 olduğundan sıfır hipotezi rədd edilə bilər. Yəni, yaş dəyişəninin maaş üzərində təsirinin olmadığını göstərən sıfır hipotezi rədd edilir. 

Əmsalların statistik bağımdan əhəmiyyətli olub olmamasını test etməyin digər bir yolu, əmsallara aid porb (ehtimal) dəhərlərini diqqətə almaqdır. 95%-lik əhəmiyyətlilik dərəcəsi vəya 5%-lik xəta payı ilə əmsalları test edək. Əgər əmsallara aid prob dəyəri 0.05-dən böyük olarasa, sıfır hipotezi qəbul edilir. Əks təqdirdə isə, sıfır hipotezi rədd edilir. β₂  əmsalına aid porb dəyəri 0.0000'a bərabərdir. Prob dəyəri 0.05'dən kiçik olduğu üçün sıfır hipotezi rədd edilir. Hər iki statistik test β₂ əmsalının statistik baxımından əhəmiyyətli olduğunu göstərir.

Beləliklə, qurulan modeldən əldə edilən əmsallar həm nəzəri baxımdan, həm də statistik baxımdan əhəmiyyətlidir.

Təxmin edilən modelə əsaslanaraq, ABŞ-da 26 yaşındakı bir insanın ortalama saatlıq qazancının nə qədər olduğunu hesablamaq olar.

                               OSQ = 3.32418408995 + 0.451931318807*26=15.07

Bu modelin nəticələrinə görə ABŞ'da 26 yaşında işləyən bir insanın ortalama saatlıq qazancı ortalama olaraq 15 dollar 7 sentə bərabərdir.

Modelimiz təkdəyişənli model olduğundan Ortalama Saatlıq Qazancdakı dəyişmələrin sadəcə 2.23 faizi Yaş dəyişəni tərəfindən açıqlanır.

Təkdəyişənli Xətti Reqresiya Modelləri.

Bir tədqiqatçı olaraq aşağdakı suallara cavab axtardığmızı nəzərə alaq.

• Hər hansı bir ölkədə parlamenet müzakirələrindən sonra sipirtli içki qəbul edərək avtomobil idərə edən sürücülərə qarşı  cəzaların tətbiq edilməsi ilə əlaqəli qanun qəbul edilmişdir. Qəbul edilən bu qanunun ölümlə nəticələnən yol qəzaları üzərindəki təsiri nə qədərdir? 
• Orta məktəblərdə təhsilin keyfiyyətinin yüksəldilməsi məqsədi ilə sinifdəki şagird sayı azaldılmışdır. Bu addımın şagirdlərin test balları üzərindəki təsiri nə qədərdir?
• Universitetdə daha bir ilinizi müvəffəqiyyətlə  başa vurdunuz. Ali təhsilinizdəki bir illik atışın, gələcəkdəki maaşınızın üzərindəki təsiri nə qədər olacaq? 

Bütün bu suallardan göründüyü kimi, bir faktorun digər bir faktor üzərindəki təsiri ölçülməyə çalışılır. Başqa bir ifadə ilə desək, burada bir faktor səbəb, digər faktor isə nəticəyönümlüdür. Bu və bənzər problemlərlə qarşılaşıldığı zaman, problemin təbiətinə görə iki və ya daha çox dəyişən arasında əlaqənin araşdırılması zərurəti ortaya çıxır. Reqresiya modelləri ümumi olaraq bu tip problemlərin həllinə cavab tapmaq üçün istifadə edilməkdədir. Əgər maraqlandığımız problemdə cəmi iki dəyişən varsa, qurulan reqresiya modeli təkdəyişənli regresiya modeli, ikidən çox dəyişən varsa çoxdəyişənli reqresiya modeli istifadə edilir.  Reqresiya modellərinin təxmini üçün bir çox metod istifadə edilsə də, ekonometrik tədqiqatlarda ən çox istifadə edilən metodlar aşağıdakılardır.

• Ən Kiçik Kvadratlar Üsulu (Least Squares Method) 
• Ən Yüksək Bənzərlik Funksiyası (Maximum Likelihood Funtion)

Reqresiya modelinin təxmini üçün istifadə edilən  metodların riyazi tərəfi ilə əlaqəli açıqlamalara daha sonrakı yazılarda yer veriləcəkdir. Xətti regresyia modellərində istidadə olunacaq dəyişənlərin sayından asılı olmayaraq, dəyişənlər arasındakı əlaqənin xətti olduğu(birinci dərəcəli funksiya ilə ifadə edilə bildiyi) fərz edilməkdədir. Anakütlə ilə əlaqəli təkdəyişənli xətti reqresiya modelini ifadə edən tənlik aşağıdakı kimi göstərilə bilər.

Burada i- indeksi i=1,...,n; müşahidə(observation) dəyərlərini göstərir.

Y_i-asılı dəyişən, açıqlanan dəyişən

X_i-sərbəst dəyişən, açıqlayıcı dəyişən

β₀ anakütlə kəsişmə əmsalı(nöqtəsi)

β₁ anakütlə meyl əmsalı

u_i xəta termi

Reallıqda hər hansı modeldə istifadə olunacaq dəyişənlərin anakütlə dəyərlərini əldə etmək çox çətin olduğundan β₀  və β₁ əmsalları bilinmir. Buna görə, anakütlənin  bilinməyən əmsallarnı təxmin etmək üçün "data"lardan istifadə etmək zərurəti ortaya çıxır. 

Yuxarıda qeyd edilən suallardan yola çıxaraq təkdəyişənli xətti reqresiya modelinin necə qurulduğuna diqqət yetirək. Qurulacaq modelin məqsədi, sinifdəki şagird sayının artırılmasının, onların test nəticələrinə necə təsir etməsini araşdırmaqdan ibarətdir. Modeldə istifadə olunan datalar James H.Stock və Mark W.Watson’un   ‘http://www.pearsonhighered.com/stock_watson/’ saytından əldə edilmişdir. Datala 1998-1999 cu illər də Kaliforniya da 420 məktəbindən alınmışdır. Aşağıdakı cədvəl əldə edilən dataların paylanmasını göstərir.

Cədvəldən göründüyü kimi, ortalama şagird müəllim nisbəti 19.6, standart xəta isə 1.9’a bərabərdir. Paylanmanın 10%-lik hissəsində şagird müəllim nisbəti 17.3 olduğu halda, 90%-lik hissədə şagird müəllim nisbəti 21.9’dur. Dataların sərpilmə qrafiki aşağıda verilmişdir. 

Dəyişənlər arasında mənfi(-0.23) korrelyasiya əlaqəsi vardır. Bu isə qurulacaq modeldə şagird müəllim nisbətinin artırılmasının, şagirdlərin test balının azalmasına səbəb olacağını göstərir. 

Ekonometrik modellərin təxmini.

Ekonometrik tədqiqatlarda çox sayda paket proqram istifadə olunmaqdadır. Bunlara nümunə olaraq Eviews, STATA, SAS, Microfit, Minitab, Oxmetrics, Gauss, R, NCSS göstərmək olar. Bu blogda modellərin qiymətləndirilməsi üçün Eviews və STATA paket proqramları istifadə ediləcəkdir. Təkdəyişənli reqresiya modelinin Eviews paket proqramında təxmin edilməsinin addımları sırası ilə aşağıda verilmişdir.  Təxmin edilən model isə şagird müəllim nisbəti ilə test balı arasındakı əlaqəni analiz edən regresiya modelidir.

•  Birinci addım, istifadə ediləcək dataların olduğu 'eviews work file' açmaqdan ibarətdir. Work file açıldığı zaman qarşımıza aşağdakı şəkildə bir pəncərə çıxır. 

• Modeli təxmin etmək üçün pəncərədə görünən "Quick" menyusu və "Estimation Equation"  altmenyuları seçilir.

• Bir sonrakı addım “Equation Specification” pəncərəsində modeldə istifadə ediləcək asılı və sərbəst dəyişənlərin adlarını sırası ilə yazmaq və “Method” alt menyusundan istifadə etməklə uyğun təxmin metodunu seçməkdən ibarətdir. 
  

Qurduğumuz təkdəyişənli xətti reqresiya modelinin nəticəsi aşağıdakı kimidir.

Modelimizi dəyərləndirmək üçün yuxarıdakı cədvəli dəyərləndirməliyik. 

Dependent Variable: Asılı Dəyişən:TESTSCR-Test Score-Test Balı

Method:Least Squares: Ən Kiçik Kvadratlar Metodu

Sample: 1-420 Seçmə müşahidə aralığı 

Included observations:420 -Modelə daxil edilən müşahidə sayı

Variable:Sərbəst Dəyişən

Coefficient: Əmsal

Std.Error: Standart Xəta

t-Statistic: t statistika dəyərləri

probability: ehtimal dəyərləri

R-squared: Determinasiya əmsalı

Adjusted R-squared:  Düzəldilmiş Determinasiya əmsalı

S.E.of regression: Reqresiya modelinin standart xətası

Sum squared resid: Qalıqların kvadratları cəmi

Log likelihood: 

 F-statistic: F statistikası

Prob(F-statistic): F statistikasının ehtimalı

Mean Dependent var: Asılı dəyişənin ədədi ortası

S.D. Dependent var: Asılı dəyişənin Standart xəsası(yayınma)

Akaike information criterion- Akaike məlumat meyarı

Schwarz  criterion- Schwarz məlumat meyarı 

Hannan-Quinn criter: Hannan-Quinn meyarı

Durbin-Watson stat: Durbin Watson statistikası

Model nəticələrinə görə tənliyimizi aşağıdakı şəkildə yaza bilərik.

TESTSCR = 698.932952345 - 2.2798082879*STR

Tənlikdən göründüyü kimi şagir müəllim nisbətini göstərən STR(student teacher ratio) dəyişəni ilə test balını göstərən TESTSCR dəyişəni arasında tərsmütanasiblik var. Yəni STR dəyişənimiz bir vahid artırıldıqda TESTSCR dəyişənimiz 2.28 vahid(bal) azalacaqdır. Təxmin edilən reqresiya modelini ifadə edən xətdən də göründüyü kimi dəyişənlər arasında tərsyönlü əlaqə mövcuddur.

Təxmin edilən modelə görə hər sinifdə iki şagird artarsa, şagirdlərin test nəticələrində 4.56 (2*(-2.28))bal azalma olacaqdır.  Mənfi meyl əmsalının əldə edilməsi hər bir müəllimə düşən tələbə sayı artdıqca şagirdlərin test balının azalacağını ifadə edir. Bu məlumatlara sahib olduqdan sonra şagird sayı böyük olan siniflərdə şagird sayının dəyişməsi ilə şagirdlərin test ballarını proqnozlaşdırmaq olar. Nümunə olaraq, sinifdə 20 nəfərin olduğunu fərz edərsək, sinifin test balının 698.9-2.28*20=653.3 olacağını hesablamaq olar. Bu nəticə sadəcə test ballarına şagird müəllim nisbətinin təsir ettiyini düşündüyümüz zaman doğrudur. 

Reqresiya modeli təxmin edildikdən sonra, təxmin edilən əmsalların böyük vəya kiçik olduğunu nəzrədən keçirmək lazımdır. Meyl əmsalının böyük və ya kiçik olduğunu öyrənmək üçün başda qoyulan problemə təkrar geri qayıtmaq lazımdır. Məktəbin Kaliforniya məktəbləri arasında medyana görə ortalama bir məktəb olduğunu fərz edək. Yəni məktəbin orta balı 654.5, şagird müəllim nisbəti isə 19.7dir. Şagird müəllim nisbətinin 2 vahid azalması, bu məktəbi 50%lik hissədən, 10%lik hissəyə keçməsinə səbəb olacaqdır. Bu nəticə çox böyük dəyişmədir. Bir sonrakı sual, bu dəyişmənin şagirdlərin test balına necə təsir edəcəyi ilə əlaqəlidir. Şagird müəllim nisbətini 2 vahid azaltmaq, şagirdlərin test nəticələrini 4.6 bal artacaqdır. Bununla da, məktəbin ortalama balı 654.5 baldan 659.1 bala yüksələcəkdir. Nəticə etibarı ilə məktəbin test ballarının 50%lik hissədən 60%lik hissəyə keçirmişdir. Dataların sərpilmə qrafikinə diqqət edərsək, ən kiçik şagird müəllim nisbətinin 14 olduğunu görə bilərik. Bu dataları istifadə edərək şagird müəllim nisbəti çox kiçik olan məktəblərlə əlaqəli test nəticələrinin necə olacağınıı proqnozlaşdırmaq olmaz.

İzahlı Ekonometrik Terminlər Lüğəti

Lüğət Ekonometriyanın bütün sahələri üçün nəzərdə tutulub və daim yenilənəcəkdir.

A

Termin	İzahat	İngilis dilindəki qarşılığı
Açıqlanan Kvadratlar Cəmi	Yi’nin təxmin edilən dəyəri Y^ öz ortalamasından yayınmalarının kvadratları cəmi.	Explained Sum of Squares- ESS
Açıqlayıcı Dəyişən	Reqresiya modelindəki açıqlayıcı dəyişən, sərbəst dəyişən	Explanatory Variable, Regressor
ADL(P,Q)	Avtoreqresiv  dağıdılmış(paylanmış) gecikmə. p asılı dəyişənin gecikmələrini, q isə sərbəst dəyişənlərin gecikmələrini göstərir.	Autoregressiv Distributed Lag
Ağırlıqlı(Çəkili) Ən Kiçik Kvadratlar	Reqresiya xətəsının dəyişən varyans göstərməsi və dəyişən varyansın şəklinin bilinməsi və ya təxmin ediləbilməsi şərti altında ƏKK üsuluna alternatif olaraq istifadə edilən metoddur.	Weighted Least Square
Akaike Məlumat Meyarı	Qurulan bir neçə reqresiya modeli arasından ən yaxşı modeli seçməyə kömək edən meyardır.	Akaike Information Criteria
Alternatif Hipotez	Sıfır hipotezinin doğru olmadığı zaman, doğru qəbul edilən hipotez. Alternatif Hipotez H1 ilə göstərilir.	Alternative Hypothesis
Ana Kütlə	Hər hansı bir tədqiqat obyektində bir bütünü ifadə edir. Məs: Azərbaycandakı bütün universitet tələbələri.	Population
Avtoreqresiya	Asılı dəyişənin öz gecikmələri üzərində qurulan reqresiya. AR(p) asılı dəyişənin p gecikməsi üzərinə qurulan reqresiya modelidir.	Avtoregression-AR(p)
Avto Reqresiv Şətli Variyasiya	Şərtli dəyişən varyansın zaman sırası modelidir.	Auto Regressif Conditional Heteroskedasticity-ARCH
Asılı Dəyişən	Reqresiya və ya digər statistik modellərdə  açıqlanan dəyişəndir.	Dependent Variable
Asimptotik Paylanma	Bir təsadüfi dəyişənin, böyük həcimli seçmələr istifadə edərək əldə edilən təxmini seçmə paylanması. Nümunə olaraq. Böyük həcmli seçmələrin seçmə paylanması normal paylanmaya uyğundur.	Asiptotik Distribution
Avtokorelyasiya	Zaman sırası dəyişəni ilə bu dəyişənin gecikmiş dəyərləri arasındakı korelyasiya	Autocorrelation
Avtokovaryasiya	Zaman sırası dəyişəni ilə bu dəyişənin gecikmiş dəyərləri arasındakı kovaryasiya	Autocovariation

B

Termin	İzahat	İngilis Dilindəki Qarşılığ
Bayes Məlumat Meyarı	Qurulan bir neçə reqresiya modeli arasından ən yaxşı modeli seçməyə kömək edən meyar	Bayes Information Criterion
Bərabərzamanlı tənliklərin qeyri-obyektivliyi (qərəzliliyi)	X-dən Y-yə doğru, Y-dən də X-ə doğru bir səbəbiyyət əlaqəsinin olmasını göstərir. Bərabərzamanlı səbəbiyyət kütlə reqresiya modelində X ilə xəta terimlərinin arasında koreliyasiyanın ortaya çıxmasına səbəb olur.	Simultaneous Equation Bias
Bərabərzamanlı səbəbiyyət qərəzi		Simultaneous Causality Bias
Bernoulli Paylanması	Brenoulli təsadufi dəyişəninin ehtimal paylanması	Bernoulli Distirbution
Bernoulli Təsadufi Dəyişəni	Sadəcə 0 və ya 1 dəyəri alabilən dəyişən	Bernoulli Random Variable
Birinci Fərq	Zaman sırası dəyişəninin birinci fərqidir. Dəyişənin t anındakı dəyərindən t-1 anındakı dəyərinin fərqinə bərabərdir. Yt-Yt-1 və ya D(Yt) ilə ifadə edilir.	First Differance
Birinci Gecikmə	Zaman sırası dəyişəninin birinci gecikməsidir. Cari zaman anından bir öncəki zaman anını göstərir. Yt-1 və ya L(Yt) ilə ifadə edilir.	First Lag
Birinci Tip Xəta	Hipotez testində sıfır hipotezi doğru olduğu təqdirdə rədd edilməsindən qaynaqlanan xəta	Type I error
Böyük Ədədlər Qanunu	Bu qanuna görə örnək həcmi böyük olduğunda, örnək həcminin ədədi ortası çox böyük ehtimalla ana kütlə ortalamasına yaxınlaşır.	Law Of Large Numbers

 Ç

Termin	İzahat	İngilis dilindəki qarşılığı
Çou Testi	Zaman sırası reqresiya modellərində qırılmann bilindiyi bir tarixə görə sınanması	Chow Test
Çoxdəyişənli Xətti Regresyia Modeli	Tək dəyişənli regresiya modelinin, Y’nin k ədəd sərbəst(açıqlayıcı) dəyişənə aslılı olmasına imkan verəcək şəkildə genişlədilmiş halı	Multiple Regression Model

D

Termin	İzahat	İngilis dilindəki qarşılığı
Daxil Edilmiş Ekzogen Dəyişənlər	Xəta termini ilə korelyasiyası olmayan sərbəst dəyişənlərdir (Alət Dəyişən Reqresiya modellərində istifadə edilir).	Included Exogenous Variables
Daxil Edilmiş Endogen Dəyişənlər	Xəta termini ilə korelyasiyası olan sərbəst dəyişənlərdir (Alət Dəyişən Reqresiya modellərində istifadə edilir)	Included Endogenous Variables
Determinasiya Əmsalı	Reqresiya modelində sərbəst dəyişənlərin, asılı dəyişəni açıqlama gücünü göstərir. R2 ilə ifadə olunub [0,1] dəyərlərini alır	Cofficient of Determination
Deterministik Trend	Bir dəyişənin zaman içində, zamanın təsadüfi olmayan funksiyası olaraq göstəriləbilən uzunmüddətli hərəkətlərini ifadə edir	Deterministic Trend
Dickey-Fuller Testi	Birinci dərəcədən avtoreqresiya [AR(1)] modelində vahid kökün  varlığını yoxlamaq üçün tətbiq edilən metoddur	Dickey-Fuller Test
Dinamik Vuruq (Dinamik Multiplikator)	h-müddət dinamik vuruq zaman sırası dəyişənləri Xt dəki bir vahid dəyişmənin Yt+h üzərindəki təsiridir	Dynamic Multiplier
Dinamik Səbəbiyyət Təsiri	Bir dəyişənin, başqa bir dəyişənin cai və gələcək dəyərləri üzərindəki təsiri	Dynamic Causal Effect
Düzəldilmiş R2	Reqresiya modelinə yeni bir sərbəst dəyişən əlavə edildiyində, dəyəri artmayan R2	Adjusted R2

Ə

Termin	İzahat	İngilis dilindəki qarşılığı
Əksik müəyyənləşdirmə	Alət dəyişənlərin sayının, endogen sərbəst dəyişənlərin sayından az olması	Underidentification
Ən yaxşı xətti yayınması olmayan təxminedici (qiymətləndirici)	Y-nin müşahidə dəyərlərininxətti funksiyası olan təxmincilər arasında ən kiçik varyasiyaya sahib və yayınması olmayan təxminci. Qauss-Markov şərtləri altında, ƏKK təxmincisisətbəst dəyişənlərin dəyərlərinə görə şərli olaraq əldə edilən reqresiya əmsallarının ən yaxşı xətti yayınması olmayan təxmincisidir	Best Linear Unbiased Estimator.(BLUE)
Ən Kiçik Kvadratlar Təxmincisi	Kvadratları alınmış xəta terimlərinin cəminin minumum dəyərinin tapılması ilə əldə edilən təxminci	Least Squares Estimator

İ

Termin	İzahat	İngilis dilindəki qarşılığı
İkinci Tip Xəta	Hipotez testində sıfır hipotezinin səhv olmasına rəğmən rədd edilməməsidən(qəbuledilməsi) qaynaqlanan xəta	Type II error
İki Mərhələli ƏKK		Two Stage Least Squares
İki Dəyərli Dəyişən	0 və ya 1 dəyərini alan dəyişən.	Binary Variable
İki Dəyişənli Normal Paylanma	Normal dağılımın iki dəyişənin birgə paylanmalarını göstərən paylanma	Bivariate Normal Distribution
İki Tərəfli Alternatif Hipotez	Alternatif hipotezdə, tədqiq edilən parametrin sıfır hipotezində verilən dəyərə bərabər olmaması	Two-sides alternative hypothesis