Qeyri Xətti Reqresiya Modelinin Təxmini

İqtisadi dəyişənlər arasındakı əlaqə heç də həmişə xətti şəkildə olmur. Modeldə istifadə edilən dəyişənlər arasındakı əlaqələr, dəyişənlərin xarakterindən asılı olaraq polinomyal funksiyalar şəklində ifadə edilə bilir. İqtisadi dəyişənlər arasındakı əlaqə ümumi olaraq birinci, ikinci və ya üçüncü dərəcəli funksiyalar ilə xarakterizə edilir. Qeyri xətti reqresiya modelinə nümunə olaraq, əmlak bazarında ev qiymətləri ilə evin sahəsi (m²) arasındakı əlaqəni göstərmək olar. Bu əlaqəni kvadratik funksiya ilə ekonometrik model olaraq aşağıdakı şəkildə ifadə edəbilərik.

QEYD 1: Qeyri-xəttilik anlayışı sadəcə dəyişənlər üçün deyildir. Bir sıra modellərdə, xüsusi ilə maliyyə ekonometriyasında parametrləri zamana görə dəyişən modellərdə, parametrlər də qeyri-xətti ola bilər. 

QİYMƏT_i=β₁+β₂EVSAHƏSİ_i²+e_i

Modeldə istifadə edilən dəyişənlərə aid müşahidə sayı 1080 olub, http://principlesofeconometrics.com/poe4/poe4.htm götürülmüşdür[1]. Müşahidə dəyərləri ABŞ’ın Luiziana ştatının paytaxtı Baton Rouge’da 2005ci ilin ortalarında satışa çıxarılan evlərdən əldə edilmişdir. Dəyişənlərə aid ölçü vahidləri uğun olaraq Amerikan dolları və kvadrat futla(square feet) ifadə edilmişdir. Azərbaycan oxucusuna daha aydın olması məqsədi ilə, fut ölçü vahidi  kvadrat metr ölçü vahidi ilə ifadə edilmişdir. 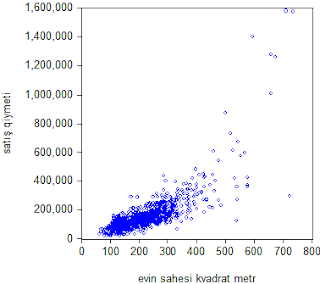Bir kvadrat futun, 0.9290304 kvadrat metrə bərabər olduğunu nəzərə alaraq evin sahəsi kvadrat metr ölçü vahidinə çevrilmişdir. Aşağıda hər iki ölçü vahidinə görə evin sahəsinin qiymətə qarşı paylanma qrafiki verilmişdir.

Qrafiklərdən aydın bir şəkildə göründüyü kimi evin sahəsinin ölçü vahidi dəyişsə də, qiymətə qarşı paylanma qrafikində həransı bir dəyişiklik yoxdur.

Nəzəri və praktik baxımdan evin qiymətinə təsir edən digər faktorlar olsa da, bu modeldə evin qiymətinə təsir edən faktor olaraq sadəcə evin sahəsi nəzərə alınmışdır. Evin sahəsi ilə yanaşı onun qiymətinə təsir edən digər faktorların ( yataq otağı sayı, hamam otağı sayı, evin yaşı, buxarı, hovuz, memarlıq üslubu, metroya-şəhər mərkəzinə-xəstəxanaya-banklara-ticarət mərkəzlərinə yaxınığı və.s) nəzərə alındığı Hedonik modellərlə əlaqəli gələcək yazılarımdan birində xüsusi yer ayıracağam.

Modeli təxmin etməzdən əvvəl bir neçə anlayışla tanış olaq.

Elastiklik Əmsalı- sərbəst dəyişəndə meydana gələn bir faizlik dəyişməyə(artma və ya azalma) qarşı, asılı dəyişəndə meydana gələn dəyişmənin faiz göstəricisi.

Marjinal Effekt-sərbəst dəyişəndə meydana gələn kiçik bir dəyişmənin, asılı dəyişən üzərindəki təsirini ifadə edir. Həmçinin iqtisadiyyatda funksiyanın qrafikinin meyl əmsalı marjinal effekt olaraq da adlandırılmaqdadır.

Modeli təxmin etmək üçün aşağıdakı addımlar sırası ilə yerinə yetirilir.

• 1 kvadrat fut=0.09290304 kvadrat metr olduğunu nəzərə alaraq əmrlər sətrinə scalar z=0.09290304 yazılaraq, dəyəri 0.09290304 olan bir z sabiti əldə edilir. Eviews proqramında bu sabit üçün c'dən başqa istənilən hərflə işarə edilə bilər.
• əmrlər sətrinə series eskm=z*eskf yazmaqla kvadrat fut ölçü vahidi ilə ifadə olunan evin sahəsini, kvadrat metrlə ifadə etmək olar.

Yuxarıda göstərilən əmrlər yerinə yetirildiktən sonra əmrlər sətrinə ls qiymet c eskm^2 yazmaqla  kvadratik funksiya ilə ifadə edilmiş modeli təxmin etmək olar.

Təxmin edilmiş modeldə marjinal effekt əmsalı 1.78’ə bərabərdir. Ev sahəsinin dəyişdiyini nəzərə alaraq müxtəlif ölçüyə sahib evlərin marjinal effekt əmsalını aşağıdakı şəkildə hesablamaq olar.

Yuxarda təsviri olaraq göstərilən addımlar yerinə yetirildikdən sonra istənilən sayda ev sahəsi üçün marjinal effekt əmsalı hesablamaq olar. Göstərilən nümunədə 5 fərqli ev sahəsi üçün marjinal effekt əmsalı hesablanacaqdır. Bunun üçün isə əmrlər sətrinə aşağıdakı əmrləri yazmaq kifayyətdir.

• dydx(1)=2*@coefs(2)*10

• dydx(2)=2*@coefs(2)*20
• dydx(3)=2*@coefs(2)*50 
• dydx(4)=2*@coefs(2)*80
• dydx(5)=2*@coefs(2)*100

Bu əmrlər "dydx" adı ilə qurulan 5*1 ölçülü vektorun 1ci,...,5ci sətirləridə müvafiq olaraq ev sahəsinin 10,20,...,100 kvadrat metr artdığı haldakı marjinal effekt əmsalını hesablayır. Buradakı coefs(2) isə,  təxmin edilmiş modeldəki beta2 əmsalını (1.78) ifadə edir.

Təxmin edilən modeldən ortalama marjinal effek istə aşağıdakı düsturla hesablanır.

Bu düsturu Eviews proqramında əmrlər sətrinə series me=2*@coefs(2)*eskm ilə esablamaq olar. Marjinal Effekt sırasına aid təsviri statistikaları nəzərdən keçirək.

Təsviri statistikalardan ədədi ortalama, ortalama marjinal effekti göstərir. Buna görə, verilən modeldə əlavə hər kvadrat metr ev sahəsi üçün qiymətin ortalama marjinal effekti 772.18 dollara bərabərdir. Standart xəta isə, təxmin edilmiş marjinal effektlərin nə qədər dəyişkənlik göstərdiyinin bir ölçüsüdür. 

Qiymətin ev sahəsinə görə elastikliyini də, eyni şəkildə hesablamaq olar. Marjinal effekt əmsalı kimi, elsatiklik əmsalı da verilən hər bir nöqtədə fərqli qiymətlər alır. Verilən modeldə elasitklik əmsalını hesablamaq üçün 

düsturundan istifadə edilir. Elastiklik əmsalını təxmin etmək üçün ümumi yanaşma qiymət və ev sahəsinin istifadə edildiyi reqresiya modelindən qiymət dəyişəninə aid təxmin edilmiş dəyərləri istifadə etməkdir. Bu deyilənləri Eviews proqramında tətbiq etmək üçün aşağıdakı addımlar sırası ilə yerinə yetirilir.

• işçi faylındakı mövcud olan müşahidə sayı dəyişdirilir.
• 

Marjinal Effeklərin hesablanması zamanı istifadə edilən 10,20,50,80,100 dəyərləri evsahəsi(eskm) dəyişəninin1081, 1082,...,1085 ci müşahidə dəyərləri yerinə yazılır.

• Yeni dəyərlər daxil edildikdən sonra model yenidən təxmin edilir.

Buradan əldə edilən qiymetf adlı sıra qiymət sırasının proqnoz(forecast) dəyərləridir. Qiymətin proqnoz dəyərlərindən istifadə etməklə, ev sahəsinin hər bir nöqtəsinə aid elastiklik əmsalları hesablana bilər. Bunun üçün Eviews proqramının əmrlər sətrinə aşağıdakı əmr yazılır. 

series elastiklikemsali=2*@coefs(2)*(eskm^2)/qiymetf

Son şəkildə ev sahəsinin hər bir nöqtəsi üçün qiymət elastikliyi verilmişdir. Modeldə istifadə edilən müşahidə sayına əsasən hesablanan ortalama qiymət elastikliyi isə, elastiklik əmsalı dəyişəninin təsviri statistikalarına baxmaqla görmək olar. 

Elastiklik əmsalına aid ədədi orta dəyəri(mean) 1.10' bərabərdir. Elsatiklik əmsalının ədədi ortalamasının 1.10'a bərabər olması, qiymətin ev sahəsinə görə elsatik (1.10>1) olduğunu göstərir. 

Dəyişənlərin Xətti və Qeyri Xətti(kvadratik) Reqresiya Modelinə Uyğunluq Qarafikləri aşağıdakı şəkildədir. 

Qrafikdən göründüyü kimi verilən dəyişənlər arasındakı əlaqənin təxmini qeyri xətti şəkildə ifadə edilən reqresiya modelinə daha uyğundur. 

Yarı Loqarifmik Reqresiya Modeli

Dəyişənlər arasındakı qeyri-xətti əlaqənin başqa bir növü də, Yarı Loqarifmik Reqresiya modelidir. Adından göründüyü kimi, modeldə istifadə edilən dəyişənlərdən biri, dəyişənlərdən birinin loqarifmik dəyərini, digəri isə dəyişənin ilkin dəyərini ifadə edir.  Başqa bir ifadə ilə desək, reqresiya modelinin bir tərəfindəki dəyişən, həmin dəyişənin loqarifmik dəyərlərindən ibarətdirsə, reqresiya modelinin digər tərəfində yer alan dəyişən isə dəyişənin öz dəyərlərindən ibarətdir. Yuxarıda istifadə etdiyimiz dəyişənlər ilə yarı loqarifmik model aşağıdakı şəkildə ifadə edilir. 

Log(QİYMƏT_i)=α₁+α₂EVSAHƏSİ_i+e_i

Göstərilən modeli Eviews proqramında təxmin etmək üçün, qiymət dəyişənin aldığı ilkin dəyərləri loqarfmik dəyərlərə çevirmək lazımdır. Bunun üçün proqramın əmrlər sətrinə series logqiymet=log(qiymet) əmrini yazmaq kifayyətdir. Eviews programında log əmri hər hansı bir dəyişənin natural loqarifmasını hesablayır.

Dəyişənlər arasındakı əlaqə, yarı loqarifmik reqresiya modeli ilə təxmin edilərək aşağıdakı nəticə əldə edilmişdir.

Model nəticələrini şərh edərkən, sərbəst dəyişəndəki 1%-lik dəyişmə, asılı dəyişəndə alfa2*100% qədər bir dəyişməyə səbəb olur. Yuxarıda təxmin edilən yarı loqarifmik modeldə, evin sahəsindəki 1%-lik artım, evin qiymətini 4.1 faiz (0.000411*100) artırır. 

Verilən dəyişənlərlə qurulan, xətti, kvadratik və yarı loqarifmik modellərdən hansının daha yaxşı uyğunluü göstərdiyini aşağıdakı qrafikdən görmək olar. 

Qrafikdən göründüyü kimi yarı loqarifmik şəkildə ifadə edilən reqresiya modeli müşahidə dəyərlərinə daha çox uyğunluq göstərir. Hansı modelin daha yaxşı uyğunluq göstərdiyini başqa bir şəkildə aşağıda verilən cədvəldən görmək olar. 

Dəyişənlər arasındakı əlaqəni müxtəlif funksional asılılıqla ifadə edildiyi zaman hansı modelin ən yaxşı model olduğuna qərar vermək üçün qurulan reqresiya modellərindən əldə edilən AIC(Akaike Information Criteria), SC(Schwarz Criteria) və SER(Standart Error of Regression-Reqresiya Modelinin Standart Xətası) dəyərlərininin ən kiçik olduğu model ən yaxşı model olaraq seçilir. Bu kriteriyalara görə Evin Sahəsi və Qiyməti arasındakı asılılığı funksional olaraq ən yaxşı şəkildə Yarı Loqarifmik model təmsil edir.

QEYD 2: Yuxarıdakı qrafikdən göründüyü kimi, ən böyük determinasiya əmsalı (0.69)kvadratik funksiya ilə ifadə edilmiş reqresiya modelinə aiddir. Asılı dəyişənləri fərqli olan reqresiya modelləri arasında seçim edərkən, ən yüksək determinasiya əmsalına sahib olan modeli seçmək doğru bir yol deyildir. 

AIC,SC və SER kimi dəyərləndirmə meyarlarına görə, verilən dəyişənlər arasındakı əlaqənin görsətərilməsi üçün, yarı-logarifmik model ən uyğun model kimi görünsə də, bu nəticənin də, test edilməsi zərurəti vardır. Bu kimi hallarda RAMSEY RESET(RESET-Regerssion Selection Test-Regresiya Seçim Testi) testi istifadə edilir. Bu testlə əlaqəli daha sonrakı yazılarımda yer ayıracağam.

---

[1] Məlumat Qaynağı:  Dr. Kelley Pace, Department of Finance, Louisiana State University 

Qauss Markov və Xətti Reqresiya Modelinin Şərtləri

Tədqiqatçının maraqlandığı mövzudan asılı olaraq tənlik və ya tənliklər sistemi ilə ifadə edilən ekonometrik modellərin təxmini üçün ən geniş şəkildə istifadə edilən metodlardan biri Ən Kiçik Kvadratlar Metodudur. Modelin təxmini zamanı əsas maraqlandığımız suallardan biri dəyişənlərə aid parametrlərin(əmsalların) anakütlə parametrlərini dolğun bir şəkildə ifadə edib etməməsini araşdırmaqdan ibarətdir. Təxmin edilən parametrlərin anakütlə parametrlərini reallığa yaxın  bir şəkildə təmsil etməsi üçün aşağıdakı şərtləri yerinə yetirməsi lazımdır.

1.      Yayınmamazlıq (Unbiased)

2.      Effektivlik (Efficiency)

3.      Tutarlılıq (Consistency)

Yayınmamazlıq: anakütlə parametrlərinin gözlənilən dəyəri(expected value) ilə təxmin edilən parametr(təxminci) arasındakı fərqin sıfıra bərabər olmasını ifadə edir. Əgər bu fərq sıfırdan fəqlidirsə modelin təxmini nəticəsində əldə etdiyimiz parametrlər anakütlə parametrlərindən müsbət və ya mənfi istiqamətdə kənarlaşma ilə nəticələnəcək.

Effektivlik: anakütlə parametrinin təxmin edilmiş iki və ya daha çox parametr arasından dispersiyası ən kiçik olan parametr anakütlə parametrinin effektiv təxminedicisidir.

Ttuarlılıq: anakütlə parametrinin təxmincisi yayınmamazlıq şərtini yerinə yerirməyə bilər. Ancaq,  seçmə müşahidə ölçüsü (sample size) artdıqca təxminci yayınmamazlıq şərtini yerinə yetirəcəkdir.  Bir başqa ifadə ilə desək, limit sonsuza getdikdə ana kütlə parametrinin gözlənən dəyəri və dispersiyası təxmincinin aldığı qiymətə bərabər olacaqdır.

Yuxarıda sadalanan bu şərtlər Qauss Markov şərtləri adlanır. ƏKKM ilə təxmin edilən modelin parametrləri bu şərtləri yerinə yetirir.

Xətti reqresiya modelinin aşağıdakı şərtləri yerinə yetirməsi zəruridir.

1.  Anakütlə xəta termini təsadüfi dəyişən olmaqla bərabər  gözlənən dəyəri (şərti ortalaması) sıfıra bərabərdir.

2.  Sərbəst dəyişən x’in hər bir dəyərində, xəta terminin dispersiyası sabitdir.

3. Xəta teriminləri bir biri ilə əlaqəsizdir. Yəni, xəta terminləri arasındakı kovariyasiya, dolayısı ilə koreliyasıya sıfıra bərabərdir.

4.  Xəta terminləri ilə sərbəst dəyişən arasında əlaqə yoxdur. Başqa bir şəkildə ifadə etsək xəta terminləri ilə sərbəst dəyişənlər arasında kovariyasiya sıfıra bərabərdir.

5.   Xəta termini Normal Paylanmaya sahip olmalıdır.

6.     X dəyişəninin aldığı dəyər təkrarlanan seçmələrdə sabitdir. Bu şərt reqresiya modelinin x dəyişəninə görə şərti olduğunu göstərir.

7.    X dəyişəni hər hansı bir ehtimal paylanmasına (probability distribution) sahib olmamaqla bərabər ən az iki dəyər almalıdır.

8.     Müşahidə sayı (n) dəyişən sayından çox olmalıdır.

Emprik Bir Nümunə

            Təhsil almaq hər bir vətəndaşın ən təməl haqlarından biridir. Bir çox hallarda  fərdlərin təhsil almaq istəyi müxtəlif səbəblərə görə məhdudlaşır. Fərdlərin təhsil alması və ya təhsilini istədiyi səviyyədə davam etdirməsi də, müəyyən maneələri aşmaq hesabına başa gəlir. Təhsil almaq istəyən bir fərdin qaşısındakı əngəllərdən biri də, yaşadığı yerlə təhsil alacağı yer arasındakı məsafənin böyük olmasıdır. Təhsil ocağına uzaqlıqla bağlı problemlə qarşılaşdıqda fərdlər ya təhsil almaqdan tamamən imtina edir, ya da təhsilini tam şəkildə sonlandırmır. Beləliklə, universitet və yaşayış yeri arasındakı uzaqlıq təhsilin səviyyəsinə öz mənfi təsirini göstərmiş olur.

            Modelimizdə istifadə edilən dəyişənlər də, fərdlərin tamamlanmış təhsil ili və yaşadıqları yerlə universitet arasındakı məsafəni göstərən dəyişənlərdən ibarətdir. Dəyişənlərə aid ölçü vahidləri müvafiq olaraq il və 10 mil olaraq ölçülmüşdür. Dəyişənlərə aid dəyərlər, 1980 ci ildə Amerikanın Təhsil Departamenti tərəfindən ABŞ’ın qərb bölgələrində yerləşən 1100 orta məktəbdə son sinifdə təhsil alan şagirdlər arasında keçirdiyi anket sorğusunun nəticələrindən əldə edilmişdir. Dəyişənlərə aid dəyərlərə qrafiki olaraq nəzər yetirək.

Qrafikdən göründüyü kimi təhsil ocağına uzaqlıq artdıqca müəyyən tamamlanmış təhsil ili üzrə fərdlərin sayı azalmaqdadı. Belə ki, universitetə uzaqlığı 80 mil olan fərdlər müvafiq tamamlanmış təhsil ili ətrafında daha sıx toplanmışdır. Uzaqlıq artdıqca bütün tamamlanmış təhsil ili səviyyələrində fərdlərin sayı azalmaqdadı. Bunu dəyişənlər arasındakı korelyasiya əmsalına baxaraqda müəyyən etmək olar.

Korelyasiya əmsalı dəyişənlər arasında mənfiyönlü əlaqənin olduğunu göstərsə də. Statistik baxımdan bu əlaqənin inamlılığı test edilməlidir. Bu isə qurulan təkdəyişənli modeldə müvafiq əmsalın statistik baxımdan əhəmiyyətli olub olmamasına bağlıdır.  ƏKKM'na əsasən qurulan modelin nəticəsi aşağıda verilmişdir.

Modelin nəticəsi tamamlanmış təhsil ili və məsəfə dəyişənləri arasında gözlənilən əlaqəni təsdiqləyir. Məsafə dəyişəninə aid əmsalın (-0.073373) t statistik dəyəri %95 əhəmiyyətlilik dərəcəsi, 3794 sərbəstlik dərəcəsində t kritik dəyəri 1.645 'ə bərabərdir. Məsafə dəyişəninə aid əmsalın hesablanmış t statistik dəyəri  |-5.34|>1.645 olduğu üçün əmsal statistik baxımdan əhəmiyyətlidir. Universitetə uzaqlıq bir vahid (10 mil) artdığı zaman  tamamlanmış təhsil ili 0.07 vahid azalmaqdadır. Təxmin edilən model riyazi olaraq aşağıdakı şəkildə göstərilə bilər.

TTI = 13.9558561148 - 0.0733727071292*MESAFE

Modeldən əldə edilən qalıqların (real dəyərlərlə təxmin edilmiş dəyərlər arasındakı fərq) reqresiya modelinin şərtlərini yerinə yetirib yetirmədiyini aşağıdakı şəkildə test edə bilərik.

1.Avtokorelyasiya testi: bu test modeldən əldə edilən qalıqların öz dəyərləri arasında koreliyasiyanın olub olmamasını araşdırır. Qalıqların avtokoreliyasiya  sahib olub olmamasını Durbin-Watson testi ilə test etmək olar. Durbin-Watson test dəyəri aşağıdakı düstura əsasən hesablanır.

Müşahidə sayı böyük olduğu zaman, d dəyəri 

 Buradakı "ro" koreliyasiya əmsalı 1 qiymətini aldığı zaman d=0, "ro" -1 qiymətini aldığı zaman isə d=4 qiymətini almış olur. Durbin-Watson cədvəlinə əsaslanaraq qalıqlar arasında koreliyasiya aşağıdakı şəkildə müəyyən edilir. 

1.      0<d<d_L isə müsbət avtokorelyasiya var

2.      d_L≤d≤d_U isə qərarsızlıq bölgəsi

3.      d_U≤d≤4-d_U avtokoreliyasiya yoxdur

4.      4-d_U≤d≤4-d_L qərarsızlıq bölgəsi

5.      4-d_L< isə mənfi avtokoreliyasiya var

 d_Lvə  d_U də müvafiq olaraq alt(lower) və üst(upper) limitləri göstərir. 

Durbin-Watson kritik dəyər cədvəli

Modelimizdə DW testinin hesablanmış dəyəri 1.768991'ə bərabərdir. Bu dəyərə görə modeldən əldə edilən qalıqlar arasında avtokoreliyasiyanın olub olmaması haqqında qərar vermək üçün, DW kritik dəyər cədvəlindən d_L və d_U dəyərlərini müəyyənləşdirilməlidir. Qurulan modeldə bir sərbəst dəyişən olduğundan k=1 şərti və 3474  sərbəstlik dərəcəsinə görə d_L və d_U  müvafiq olaraq 1.748 və 1.789 dəyərini alır. Qərar qrafikini yenidən tərtib edilərək modelin qalıqları arasında avtokoreliyasiyanın olub olmaması haqqında qərar verilir.

Qrafikdən göründüyü kimi modeldən əldə edilən DW dəyərinə əsaslanaraq modelin qalıqları arasında avtokoreliyasiyanın olub olmaması ilə əlaqəli qərar vermək çətindi.

Yuxarıda deyilənləri diqqətə alaraq DW test statikasının zəif tərəflərini aşağıdakı kimi göstərmək olar.

1.DW test statistikası sadəcə birinci dərəcədən avtokoreliyasiyanın olub olmadığını hesablayır.

2. Dəyişənlərdən hər hansı birinə aid bir və ya bir neçə müşahidə sayı olmadıqda DW test statistikasını hesablamaq olmur.

3. Hesablanan DW dəyəri qərarsızlıq bölgəsinə düşdükdə avtokoreliyasiyanın olub olmadığı haqqında fikir irəli sürmək çətinləşir.

Avtokoreliyasiyanın olub olmadığını tədqiq etməyin bir başqa yolu Breusch-Godfrey testidir. Eviews proqramında test aşağıda göstərilən şəkildə hesablanır. 

 Avtokoreliyasiya ilə əlaqəli hipotez testləri aşağıdakı kimidir.

H₀: Qalıqlar Arasında Avtokoreliyasiya Yoxdur

H₁: Qalıqlar Arasında Avtokorelisyasiya Vardır

Breusch-Godfrey LM test statistikasının prob dəyərləri 0.05’dən kiçik olduğu (0.000<0.05) üçün qalıqlar arasında avtokoreliyasiyanın olmadığını göstərən sıfır hipotezi rədd edilir.

2.Dəyişən Dispersiya testi: Modeldən əldə edilən qalıqların üzərinə qoyulan şərtlərdən bir də, sərbəst dəyişənlərin dəyişən dəyərlərinə qarşı qalıqların dispersiyasının dəyişməz olaraq qalmasıdır. Qalıqların dispersiyasının sabit vəya dəyişən olduğunu aşağıdakı şəkildə müəyyənləşdirmək olar.

Dəyişən dispersiyanın mövcudluğunu müəyyənləşdirən Breusch-Pagan-Godfrey(BPG), Harvey, White, Glejser testləri olsa da,  BPG testi istifadə edilmişdir. Dəyişən dispersiya ilə əlaqəli hipotez testləri aşağıdakı kimidir.

H₀: Qalıqlarda Dəyişən Dispersiya yoxdur. (Homoscedasticity)

H₁: Qalıqlarda Dəyişən Dispersiya vardır (Heteroscedasticity)

BPG testinin prob dəyəri, 0.05'dən böyük olduğu üçün sıfır hipotezi qəbul edilir. Testin nəticəsinə görə qalıqlarda dəyişən dispersiya yoxdur. 

3.Normal paylanma testi: Qalıqların yerinə yerirməsi gərəkli olan şərtlərdən biridir. Normal paylanma aşağıdakı şəkildə test edilir. 

Normal paylanmaya aid hipotez testləri aşağdakı kimidir.

H₀: Qalıqlar Normal Paylanmaya Sahibdir

H₁: Qalıqlar Normal Paylanmaya Sahip Deyil

Qalıqların histoqramına diqqət yetirildikdə paylanmanın simmetrik olmadığını görmək olar. Ayrıca, Normal paylanma testi olan Jarque-Bera test statistikasına aid prob dəyərinin 0.05 dən kiçik olduğu üçün sıfır hipotezi rədd ediləbilər. Qalıqlar Normal Paylanmaya sahib deyil. Normal Paylanma zamanı Skewness=0 Kurtosis=3 olmalıdır. Hər iki dəyər göstərilən dəyərdən fərqli olduğu üçün qalıqların Normal Paylanmaya sahib olmadığını söyləmək olar.